Результат экзамена по раскладу “Синтез”: какую оценку ждать

{RANDOM_PARAGRAPH=100-400}

Результат экзамена по раскладу “Синтез”: какую оценку ждать

Расчёт вероятности получения положительной отметки

при решении тестовых заданий по математике

Высшее назначение математики…состоит в том,

чтобы находить скрытый порядок в хаосе, который нас окружает

Однажды при подготовке к контрольной работе учитель математики задала на дом пять задач по геометрии. Четыре я решил, пятая же не получилась. Я понадеялся, что учитель спросит кого-либо другого, а если и меня, то попадется одна из четырех решенных мной задач. Но учитель вызвала именно меня и спросила как раз пятую задачу. Случайность! И на этот раз не очень-то приятная! Кажется, как можно «предвидеть» наступление случайного события? Ведь оно может произойти, а может и не сбыться!

При решении самостоятельной или контрольной работы в тестовой форме, особенно по математике, информатике, физике большинство моих одноклассников надеются, что за работу можно будет получить хорошую оценку, выбирая правильные варианты ответов интуитивно, без теоретических знаний. Поэтому я решил оценить, насколько данный метод обеспечит положительную оценку, и как результаты моего исследования по теории вероятностей можно будет практически применить при тестировании.

Актуальность

Тестирование в образовании – современный подход к оценке знаний учащихся. Тестовая форма контроля на сегодняшний день является самой востребованной: она используется на ГИА и ЕГЭ. А потому, чем раньше мы начнем приобщаться к такой форме проверки знаний, тем лучше будем подготовлены к итоговой аттестации и различного рода испытаниям в тестовой форме.

Вероятность угадать верные ответы при тестировании очень мала, а значит практически невозможно получить положительную оценку без подготовки.

Определить вероятность получения положительной отметки при написании тестов по математике путем угадывания правильного ответа.

Для реализации цели были поставлены следующие задачи:

1) собрать, изучить и систематизировать материал о теории вероятностей, воспользовавшись различными источниками информации;

2) провести статистический эксперимент;

3) проанализировать результаты тестовых работ с применением теории вероятности.

Объект исследования: теория вероятности.

Предмет исследования: тесты по математике.

Методы исследования: анализ, синтез, сбор информации, анкетирование работа с литературой, эксперимент.

Практическая значимость данной работы состоит в том, что она нацелена помочь обучающимся осознать важность учения, так как согласно проведенному исследованию получить положительную отметку за тестовую работу путем угадывания мало вероятна.

Теоретическая часть

Глава 1. Теория вероятностей

История возникновения.

Теория вероятностей – раздел математики, изучающий случайность. Теория вероятностей используется в таких разделах математики как математическая статистика, теория случайных процессов, теория массового обслуживания. Она находит применение в физике, в анализе азартных игр, в страховании и в расчете пенсионных схем. На теории вероятностей основана разработка, применение и анализ вероятностных алгоритмов [1].

Как наука, теория вероятностей зародилась в середине XVII века с появлением азартных игр, таких как карты и кости, когда начали применять в них количественные подсчеты и прогнозирование шансов на успех. А зарождение теории вероятностей началось с того, что придворный французского короля, шевалье (кавалер) де Мерэ (1607-1648г. г. ), сам азартный игрок, обратился к французскому физику, математику и философу Блезу Паскалю (1623-1662г. г.) с вопросами к задаче об очках. (см. главы «Формулировки и основные понятия», «Примеры и решения практических задач на вероятность»). Паскаль обратился к математику Пьеру Ферма (1601-1665г. г.) и переписывался с ним по поводу этих задач. Они вдвоем установили некоторые основные положения теории вероятностей, в частности пришли к понятию математического ожидания и теоремам сложения и умножения вероятностей.

Другим толчком для развития теории вероятностей послужило страховое дело, а именно с конца XVII века на научной основе стало производиться страхование от несчастных случаев и стихийных бедствий. В XVI-XVII веках во всех странах Западной Европы получило распространение страхование судов и страхование от пожаров. В XVII веке были созданы многочисленные страховые компании и лотереи в Италии, Фландрии, Нидерландах. Затем методы теории вероятностей стали широко применять в демографии, например, при ведении статистики рождения и смерти.

Первооткрывателями теории вероятностей считаются французские ученые Б. Паскаль и П. Ферма и голландский ученый Х. Гюйгенс (1629-1695г. г.). Стала зарождаться новая наука, вырисовываться ее специфика и методология: определения, теоремы, методы. Также теория вероятностей связана с именами известных математиков: швейцарца Якоба Бернулли (1654-1705г.г.), француза П. С. Лапласа, англичанина А. Муавра (1667-1754г. г. ) и др. Вклад в развитие теории вероятностей внесли русские и советские ученые П. Л. Чебышев, А. А. Марков, А. М Ляпунов и многие другие [2].

В XX веке выяснилось, что эта, казалось бы, легкомысленная наука играет важную роль в познании фундаментальных процессов, протекающих в микромире. Была создана современная теория вероятностей [3] .

Основные понятия теории вероятностей

Основными понятиями в теории вероятностей являются испытание, событие и вероятность.

Испытание – это эксперимент, проводимый над объектом в комплексе определенных условий.

Событие – это случай или факт, который произошел или не произошел в результате испытания.

Вероятность – это численная мера степени объективной возможности наступления события.

Вероятностью события А называется отношение числа случаев наступления этого события к общему числу случаев:

, P ( A ) – вероятность события A , m – число случаев наступления события А, n – общее число случаев, m , 0. Данное определение принято называть классическим определением вероятности . Оно применяется, когда теоретически удается выявить все равновозможные исходы испытания и определить благоприятствующие исследуемому испытанию исходы.

При изучении явлений, мы проводим эксперименты, в ходе которых происходят различные события, среди которых различают: достоверные, случайные, невозможные, равновероятные.

Событие U называют достоверным по отношению к некоторому испытанию, если в ходе этого испытания событие U обязательно произойдет. Например, достоверным будет появление одного из шести чисел 1,2,3,4,5,6 при одном бросании игральной кости.

Событие называют случайным по отношению к некоторому испытанию, если в ходе этого испытания оно может произойти, а может и не произойти. Событие V называют невозможным по отношению к некоторому испытанию, если в ходе этого испытания событие V не произойдет .

Равновероятные события – это события, которые при данных условиях имеют одинаковые шансы для наступления.

Но встречаются случаи, когда без практики определить число благоприятных исходов невозможно. В таких случаях используется статистическое определение вероятности.

Статистическая вероятность (частота, относительная частота) –это отношение числа испытаний, в которых событие появилось к общему числу фактически произведенных испытаний. Определяется следующей формулой для события: P ( A ) = , где n – общее число фактически проведенных испытаний, m – число появлений событий. Другими словами, статистическая вероятность – это вероятность события, рассчитанная опытным путем.

Формула Бернулли – это формула в теории вероятностей, позволяющая находить вероятность появления события A при независимых испытаниях. Формула названа в честь выдающегося швейцарского математика Якоба Бернулли [4].

Теория вероятности в жизни

Людей всегда интересовало будущее. Человечество во все времена искало способ его предугадать, или спланировать. В разное время разными способами. В жизни мы часто сталкиваемся со случайными явлениями. Чем обусловлена их случайность – нашим незнанием истинных причин происходящего или случайность лежит в основе многих явлений? Случайным ли образом возникают мутации, насколько зависит историческое развитие от отдельной личности, можно ли считать Вселенную случайным отклонением от законов сохранения? [2]

Примеров реального использования теории вероятности в жизни множество. Практически вся современная экономика базируется на ней. Невозможно представить без теории вероятности жизнь брокеров на мировых рынках. Предсказывание денежного курса на денежных опционах дает возможность зарабатывать на данной теории серьезные деньги.

Теория вероятности имеет значение в начале практически любой деятельности, а также ее регулирования. Благодаря оценке шансов той или иной неполадки (например, космического корабля), мы знаем, какие усилия нам нужно приложить, что именно проверить, что вообще ожидать в тысячи километров от Земли. Возможности теракта в метрополитене, экономического кризиса или ядерной войны – все это можно выразить в процентах.

Таким образом, теорию вероятностей нельзя не применять в нашей жизни. Она имеет разные области применения такие как: биологические и химические процессы, история, экономика, кораблестроение и машиностроение, медицина и большинство различной деятельности человека. Люди применяют её как сознательно, так и подсознательно, что проявляется в обычных повседневных фразах и действиях. Разумный человек должен стремиться мыслить, исходя из законов вероятностей. Теория вероятностей – это одна из составляющих частей успеха. Если стремиться учитывать законы вероятностей и, в том случае, если вероятность неблагоприятная, предпринимать соответствующие контрдействия, то можно упростить себе жизнь в разы и сэкономить своё время, которое так ценно для каждого из нас [5].

Вероятностно–статистические методы играют важную роль в практической деятельности – это контроль качества продукции, техническая диагностика оборудования, технология производства, обеспечения надежности оборудования, организация массового обслуживания, военное дело (стрельба, бомбометание, тактика, теория боеприпасов), получение достоверных результатов измерений, астрономические наблюдения и многое другое.

Глава 2. Практическая часть

2.1 Исследование

Сейчас обучение в любом классе начинается с входного тестирования, сопровождается текущим контролем с помощью заданий в тестовой форме и заканчивается объективным тестированием учебных достижений .

Кроме того, тесты позволяют наладить самоконтроль – самую полезную для обучения и гуманную форму контроля знаний, а также организовать рейтинг – эффективное средство повышения учебной мотивации.

Мы провели социологический опрос среди учащихся 7-9 классов. В связи малой накаляемостью учащихся в классах нашей школы (5-6 учащихся – средняя накаляемость класса), в анкетировании принимали участие 15 человек. Учащимся предложили ответить на вопросы:

можно ли сдать тест, экзамен без подготовки методом угадывания?

можно ли угадать, например, 6 заданий из 10, таким образом, решив тестовое задание по математике без подготовки?

По первому вопросу из 15 респондентов 9 человек (60%) ответили «да», 6 человек ( 40%) ответили «нет», т. е. считают, что таким способом сдать экзамен или решить тест нельзя.

По второму вопросу результаты такие: 80% учащихся 7 класса считают, что можно угадать 6 заданий из 10, 8кл. – 60%, 9кл. – 33%.

Вывод: чем старше класс, тем меньше веры в случай. (Приложение 1)

2.2 Теоретический расчет успешного решения тестового задания

Определить вероятность угадывания верного ответа можно по формуле Бернулли.

Пусть событие А – это правильно выбранный ответ из четырех предложенных в одном задании теста. Вероятность события А определена как отношение числа случаев, благоприятствующих этому событию (т.е. правильно угаданный ответ, а таких случаев 1), к числу всех случаев (таких случаев 4).

Тогда p=1/4, а q=1-p=3/4.

Вероятность получения положительной оценки:

Р₁₀(5)=252 = 0,0583991 0,058

То есть, вероятность благополучного исхода очень низкая, примерно 5,8%

Вывод: мало шансов решить тест или сдать экзамен на положительную оценку без подготовки. Из 10000 человек только 5- 6 могут получить положительную оценку.

2.3 Эксперимент: расчет вероятности получения положительной отметки по алгебре

Для подтверждения гипотезы исследования в 7-9 классах мы воспользовались материалами сайта «Контроль знаний» [6]. Учащимся предложили решить тесты по алгебре по следующим темам 1 :

Тест по алгебре 7 класс: Степень и её свойства (10 вопросов) 2

Тест по алгебре 8 класс: «Решение неравенств с одной переменной» (10 вопросов) 3 .

Алгебра 9: Квадратный трехчлен(10 вопросов) 4 .

В каждом тесте 10 заданий с выбором ответа по алгебре. Один ответ из четырех верный. Чтобы получить положительную оценку необходимо правильно угадать 6 ответов (60%).

Результаты эксперимента показывают, что угадал 6 ответов только один ученик (Приложение 2).

Произведем расчеты по формуле.

Пусть событие А– это правильно выбранный ответ из четырех предложенных в одном задании. Вероятность события Аопределена как отношение числа случаев, благоприятствующих этому событию (то есть правильно угаданный ответ, а таких случаев 1), к числу всех случаев (таких случаев 4). Тогда p = P(A)=1/4.

Вероятность противоположного события q = P(Ā)=1- p = 3/4.

Вероятность получения положительной отметки вычислим по формуле Бернулли, где n = 10, m = 6.

Вероятность получения положительной оценки:

Р₁₀(6) = 210 = 0,016222 0,02

Таким образом, максимальное количество правильно угаданных ответов

равно 4, что не позволяет ученику получить положительную отметку за тест по алгебре. Это же подтверждают теоретические вычисления – вероятность угадывания правильных ответов – достаточно мала, в данном случае только 0,02.. Процент правильно угаданных ответов – 13,3% (Приложение 2).

2.4 Эксперимент: расчет вероятности получения положительной отметки по геометрии

При повторном эксперименте учащимся предложили решить тесты по геометрии по следующим темам:

Геометрия 7 класс. Свойства параллельных прямых 5 .

Геометрия 8. Признаки подобия треугольников 6

Геометрия 9. Треугольники 7

В каждом тесте 12 заданий с выбором ответа по геометрии. Один ответ из четырех верный. Чтобы получить положительную оценку необходимо правильно угадать не менее 50% от всего теста, т.е. угадать не менее 6 ответов.

Вероятность получения положительной отметки вычислим по формуле Бернулли, где n = 12, m = 6.

Вероятность получения положительной оценки:

Р₁₂(6) = 924 = 0,0401494 0,04. Вероятность угадывания правильных ответов выше, чем в первом эксперименте. Процент правильно угаданных ответов 17% (Приложение 3).

Вывод: данные теории вероятностей и результаты эксперимента показывают, что способом угадывания правильного ответа в тестовом задании по алгебре и геометрии получить положительную отметку почти невозможно.

В результате проделанной работы, были достигнуты поставленные задачи:

была изучена научная литература по теме «Теория вероятностей» – это огромный раздел науки математики;

в ходе работы был проведен эксперимент, позволяющий определить вероятность успешного выполнения тестов по математике обучающимися 7-9 классов путем угадывания правильного ответа, применяя теорию вероятностей.

При проведении эксперимента наибольший процент правильно угаданных ответов был получен при написании тестовой работы по геометрии. Это, возможно, связано с тем, что обучающиеся использовали те знания, которые они получили на уроках и в повседневной жизни. Им было легче сориентироваться при выборе ответа, на уровне подсознания.

Таким образом, ранее выдвинутая гипотеза нашла свое подтверждение в проведенном исследовании. Полученные данные позволяют сделать вывод, что только планомерная, вдумчивая и добросовестная учеба в школе позволит учащимся успешно писать тестовые контрольные работы, хорошо подготовиться к участию в ГИА и успешно решить судьбоносную проблему при переходе на более высокий уровень обучения в ВУЗ.

С результатами данного исследования можно ознакомить будущих выпускников во время проведения классных часов, внеклассных мероприятий, с целью пропаганды подготовки их к экзаменам.

Результаты практических экспериментов и их теоретическое обоснование подтверждают правильность выдвинутой гипотезы.

Савельева Р. Ю. Основы теории вероятностей и математической статистики [Электронный ресурс]. – Режим доступа: http://открытыйурок.рф/статьи/526665/ (дата обращения – 24.01.2018)

Гатауллина Л. Теория вероятности в жизни [Электронный ресурс]. – Режим доступа: https://nsportal.ru/ap/library/nauchno-tekhnicheskoe-tvorchestvo/2012/01/07/teoriya-veroyatnosti-v-zhizni (дата обращения – 6.02.2018)

Кибзун А. И. Теория вероятностей и математическая статистика. Базовый курс с примерами и задачами [Текст]: учебное пособие/А. И. Кибзун, Е. Р. Горяинова, А. В. Наумов, А. Н. Сиротин. – Москва: ФИЗМАТЛИТ, 2002. – 224 с.

Теория вероятностей и основные понятия теории [Электронный ресурс]. – Режим доступа: https://bookmaker-ratings.ru/wiki/teoriya-veroyatnostej-i-osnovny-e-ponyatiya-teorii/ (дата обращения 24.01.2018)

Вишня Ю. Теория вероятности в жизни [Электронный ресурс]. – Режим доступа: https://allowwonder.com/teoriya-veroyatnosti-v-zhizni/ (дата обращения – 6.02.2018)

Можно ли сдать тест, экзамен без подготовки методом угадывания?

Рис. 1. Результаты анкетирования респондентов

Можно ли угадать, например, 6 заданий из 10, таким образом, решив тестовое задание по математике без подготовки?

Результаты статистического эксперимента: выбор учащимися 7-9 классов правильного ответа в тесте по алгебре

Онлайн гадание

Инструкция для Онлайн гадания

Несмотря на кажущуюся простоту, гадание в конечном счете, это ритуал предсказывающий судьбу. Онлайн версия любого гадания
безусловно это менее серьезная процедура, чем скажем реальное гадание на картах Таро, но если вы хотите получить максимально
точный результат предлагаем Вам выполнить ряд несложных правил перед тем как начинать процесс гадания:

1. Перед началом гадания обязательно сосредоточьтесь на своем вопросе, подумайте что точно вы хотите знать.

2. Во время гадания важно находиться в спокойной обстановке, так чтобы Вам никто не мешал.

3. Для большей концентрации, сосчитайте до 10 и сделайте 2-3 глубоких выдоха и вдоха.

4. Очень полезно задумать наперед то время через которое вы хотите чтобы сбылось гадание.

5. Не стоит повторять более двух раз одно и тоже гадание — карты будут врать. Попробуйте другое гадание и немного измените
или уточните вопрос!

6. Даже отрицательный ответ гадания воспринимайте как позитивный. Помните, что не делается — всё к лучшему!

7. И помните: Вы и только вы решаете, каким будет Ваше будущее! Вы получили прогноз, а как действовать зависит
только от Вас.

Этапы подготовки к ОГЭ за месяц

1. Скачайте варианты (купите печатные сборники с вариантами) по каждому предмету, который сдаете, и выполните их с таймером, как если бы это было на экзамене. Цель этого этапа ⎯ оценить ваш уровень знаний до подготовки к ОГЭ, списывать и обманывать себя бесполезно.

2. Проанализируйте результаты вашего пробного экзамена, выделите задания, с которыми возникли проблемы с точки зрения формулировки или содержания. Затем ознакомьтесь с кодификатором ОГЭ по каждому предмету (иначе ⎯ списком тем, которые спросят на экзамене. Он есть на сайте https://fipi.ru/oge. Оцените, какую долю во всем объеме материала занимают темы, в которых вы плохо разбираетесь. На них нужно будет делать упор следующие 30 дней.

3. Возьмите блокнот или ежедневник. В нем составьте расписание, которое будет учитывать сон, занятия спортом, прогулки, школьные уроки и приемы пищи. Оставшееся время по максимуму займите подготовкой к ОГЭ: повторением конспектов, решением задач, изучением нового материала. Не отступайте от него, а если нарушили ⎯ компенсируйте учебное время, но не превращайте это в наказание.

4. Периодически (раз в неделю) устраивайте себе повторные «пробники», чтобы следить за прогрессом. Перед экзаменом важно тренировать ощущение времени и работу с бланками.

Фотосинтез

По типу питания живые организмы делятся на автотрофы, гетеротрофы и миксотрофы. Автотрофы (греч. αὐτός — сам + τροφ – пища) – организмы, которые самостоятельно способны синтезировать органические вещества из неорганических. Гетеротрофы (греч. ἕτερος – иной + τροφή – пища) – организмы, использующие для питания готовые органические вещества.

Наконец, миксотрофы (греч. μῖξις – смешение + τροφή – пища) – организмы, которые могут использовать как гетеротрофный, так и автотрофный способ питания. К примеру, эвглена зеленая на свету начинает фотосинтезировать, а в темноте питается гетеротрофно.

Фотосинтез

Фотосинтез (греч. φῶς – свет и σύνθεσις – синтез) – сложный химический процесс преобразования энергии квантов света в энергию химических связей. В результате фотосинтеза происходит синтез органических веществ из неорганических.

Этот процесс уникален и происходит только в растительных клетках, а также у некоторых бактерий. Фотосинтез осуществляется при участии хлорофилла (греч. χλωρός – зелёный и φύλλον – лист) – зеленого пигмента, окрашивающего органы растений в зеленый цвет. Существуют и другие вспомогательные пигменты, которые вместе с хлорофиллом выполняют светособирающую или светозащитную функции.

Ниже вы увидите сравнение строения хлорофилла и гемоглобина. Обратите внимание, что в центре молекулы хлорофилла находится ион Mg.

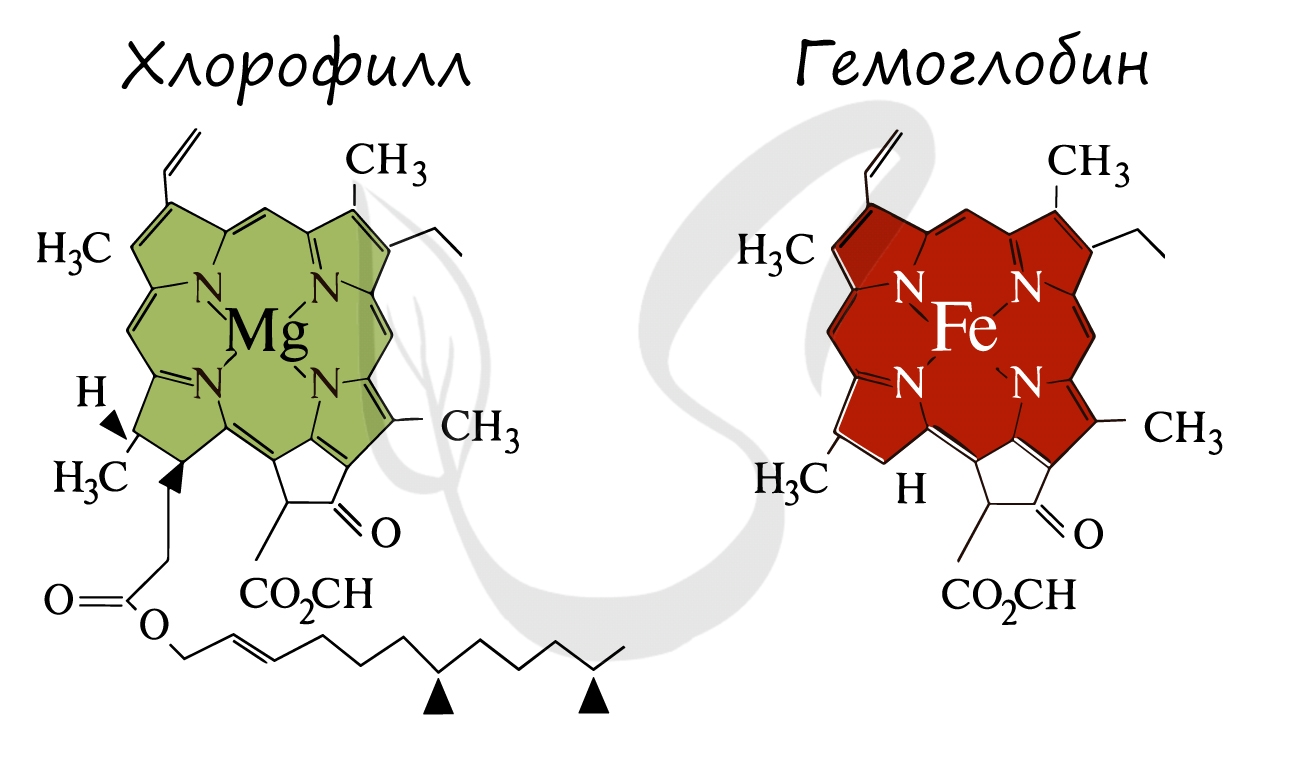
В высшей степени гениально значение процесса фотосинтеза подчеркнул русский ученый К.А. Тимирязев: “Все органические вещества, как бы они ни были разнообразны, где бы они ни встречались, в растении ли, в животном или человеке, прошли через лист, произошли от веществ, выработанных листом. Вне листа или, вернее, вне хлорофиллового зерна в природе не существует лаборатории, где бы выделялось органическое вещество. Во всех других органах и организмах оно превращается, преобразуется, только здесь оно образуется вновь из вещества неорганического”

Более подробно мы обсудим значение фотосинтеза в завершение этой статьи. Фотосинтез состоит из двух фаз: светозависимой (световой) и светонезависимой (темновой). Я рекомендую использовать названия светозависимая и светонезависимая, так как они способствуют более глубокому (и правильному!) пониманию фотосинтеза.

Светозависимая фаза (световая)

Эта фаза происходит только на свету на мембранах тилакоидов в хлоропластах. В ней принимают участие различные ферменты, белки-переносчики, молекулы АТФ-синтетазы и зеленый пигмент хлорофилл.

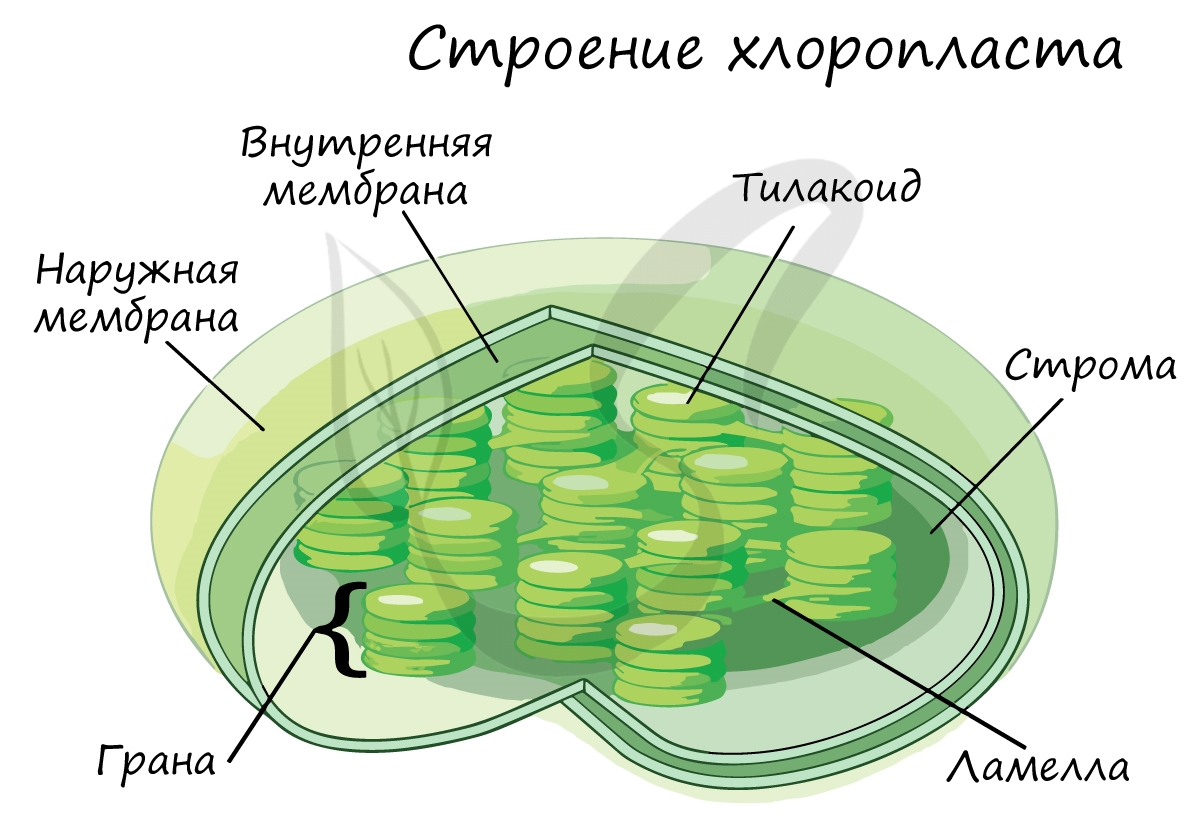
Хлорофилл выполняет две функции: поглощения и передачи энергии. При воздействии кванта света хлорофилл теряет электрон, переходя в возбужденное состояние. С помощью переносчиков электроны скапливаются с наружной поверхности мембраны тилакоидов, тем временем внутри тилакоида происходит фотолиз воды (разложение под действием света):

Гидроксид-ионы отдают лишний электрон, превращаясь в реакционно способные радикалы OH, которые собираются вместе и образуют молекулу воды и свободный кислород (это побочный продукт, который в дальнейшем удаляется в ходе газообмена).

Образовавшиеся при фотолизе воды протоны (H + ) скапливаются с внутренней стороны мембраны тилакоидов, а электроны – с внешней. В результате по обе стороны мембраны накапливаются противоположные заряды.

При достижении критической разницы, часть протонов проталкивается на внешнюю сторону мембраны через канал АТФ-синтетазы. В результате этого выделяется энергия, которая может быть использована для фосфорилирования молекул АДФ:

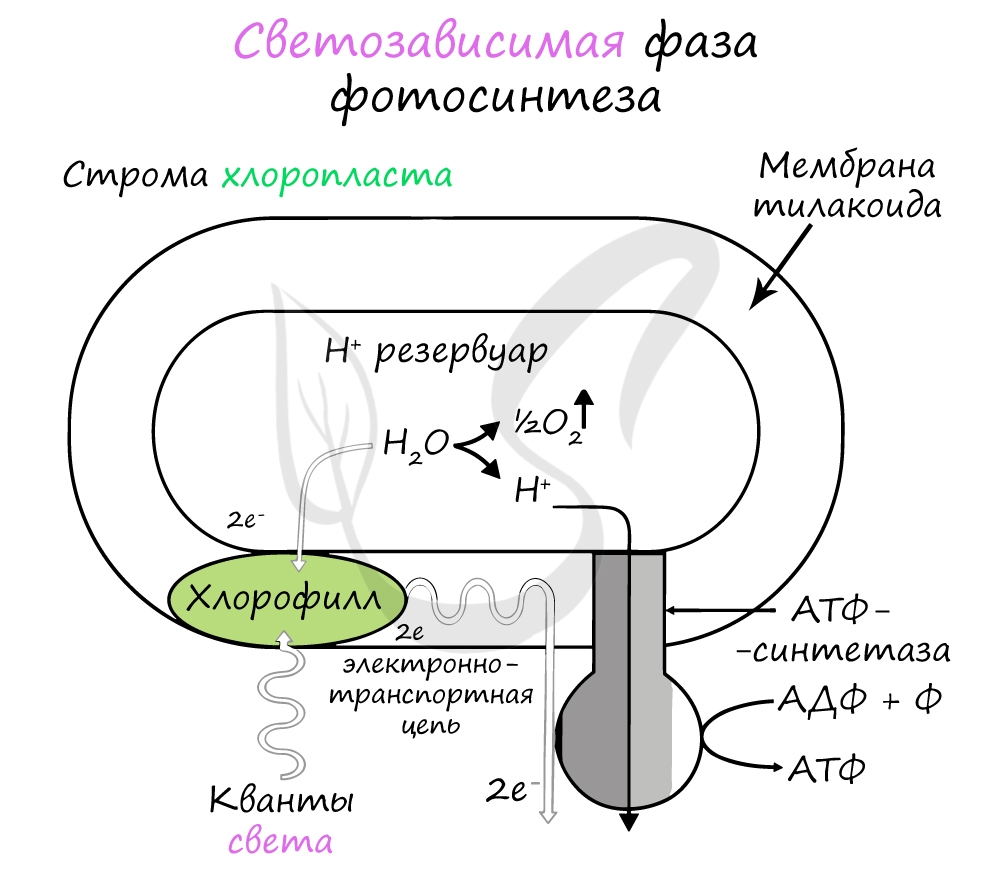
Протоны, попав на поверхность мембраны тилакоидов, соединяются с электронами и образуют атомарный водород, который используется для восстановления молекулы-переносчика НАДФ (никотинамиддинуклеотидфосфат). Благодаря этому окисленная форма – НАФД + превращается в восстановленную – НАДФ∗H₂.

• Свободный кислород O₂ – в результате фотолиза воды
• АТФ – универсальный источник энергии
• НАДФ∗H₂ – форма запасания атомов водорода

Кислород удаляется из клетки как побочный продукт фотосинтеза, он совершенно не нужен растению. АТФ и НАДФ∗H₂ в дальнейшем оказываются более полезны: они транспортируются в строму хлоропласта и принимают участие в светонезависимой фазе фотосинтеза.

Светонезависимая (темновая) фаза

Светонезависимая фаза происходит в строме (матриксе) хлоропласта постоянно: и днем, и ночью – вне зависимости от освещения.

При участии АТФ и НАДФ∗H₂ происходит восстановление CO₂ до глюкозы C₆H₁₂O₆. В светонезависимой фазе происходит цикл Кальвина, в ходе которого и образуется глюкоза. Для образования одной молекулы глюкозы требуется 6 молекул CO₂, 12 НАДФ∗H₂ и 18 АТФ.

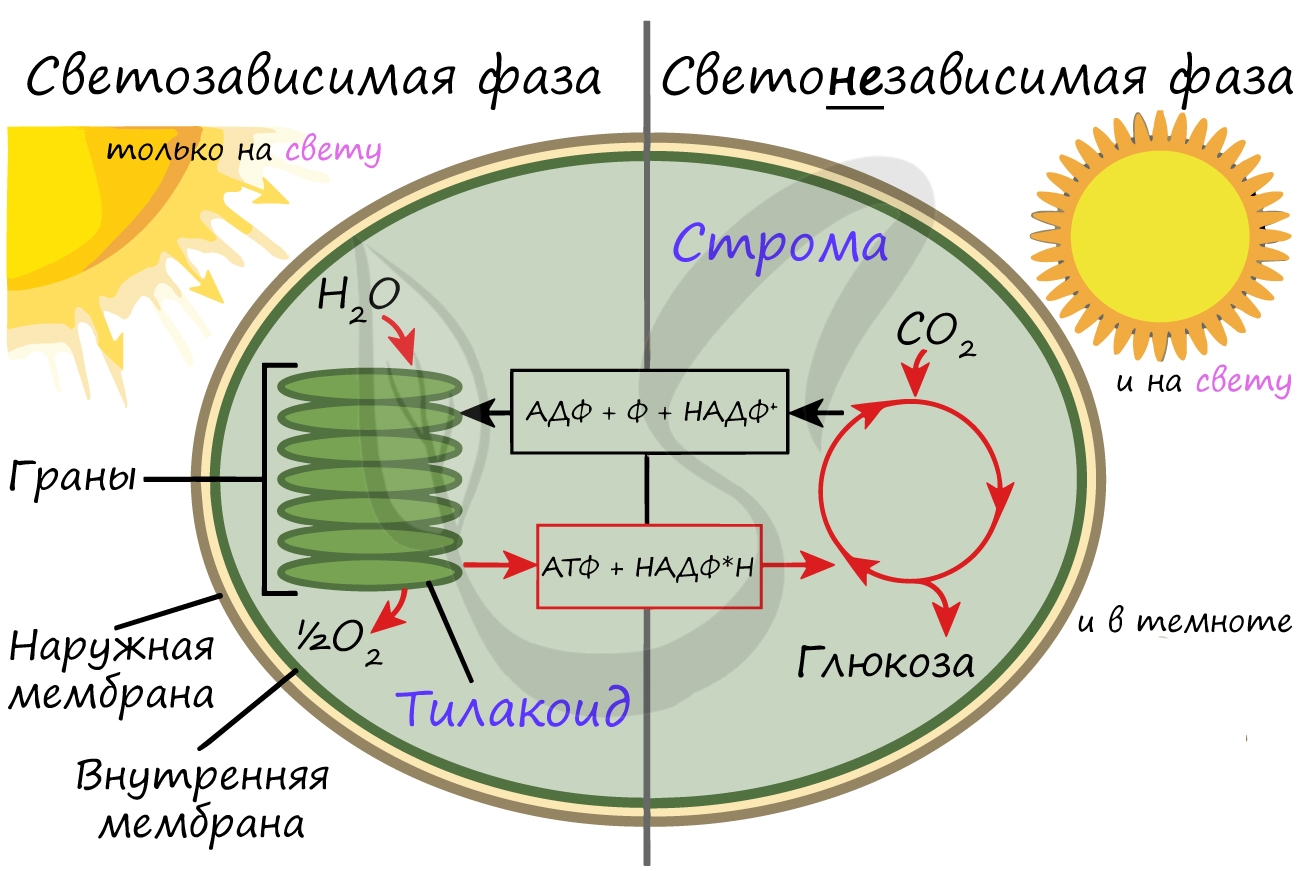
Таким образом, в результате темновой (светонезависимой) фазы фотосинтеза образуется глюкоза, которая в дальнейшем может быть преобразована в крахмал, служащий для запасания питательных веществ у растений.

Значение фотосинтеза

Значение фотосинтеза невозможно переоценить. Уверенно утверждаю: именно благодаря этому процессу жизнь на Земле приобрела такие чудесные и изумительные формы, какие мы видим вокруг себя: удивительные растения, прекрасные цветы и самые разнообразные животные.

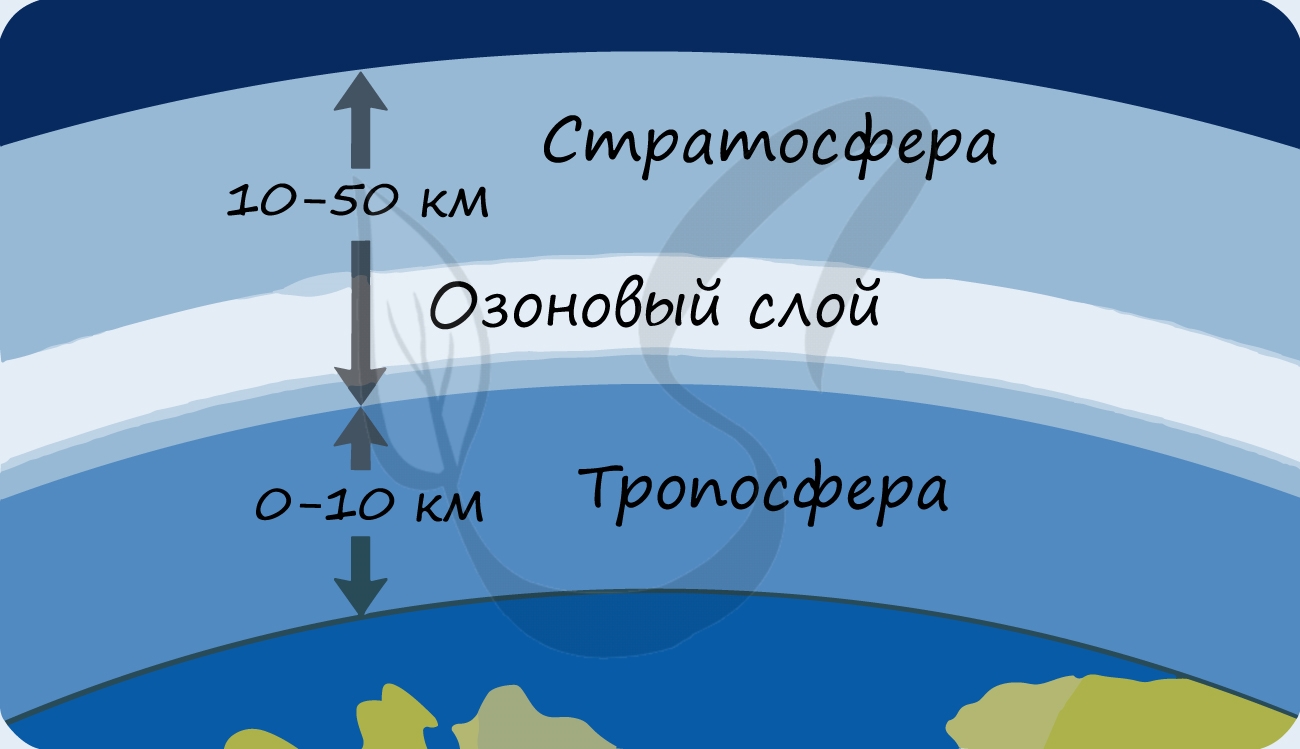
В разделе эволюции мы уже обсуждали, что изначально в составе атмосферы Земли не было кислорода: миллиарды лет назад его начали вырабатывать первые фотосинтезирующие бактерии – сине-зеленые водоросли (цианобактерии). Постепенно кислород накапливался, и со временем на Земле стало возможно аэробное (кислородное) дыхание. Возник озоновый слой, защищающий все живое на нашей планете от губительного ультрафиолета.

• Синтезируют органические вещества, являющиеся пищей для всего живого на планете
• Преобразуют энергию света в энергию химических связей, создают органическую массу
• Растения поддерживают определенный процент содержания O₂ в атмосфере, очищают ее от избытка CO₂
• Способствуют образованию защитного озонового экрана, поглощающего губительное для жизни ультрафиолетовое излучение

Хемосинтез (греч. chemeia – химия + synthesis – синтез)

Хемосинтез – автотрофный тип питания, который характерен для некоторых микроорганизмов, способных создавать органические вещества из неорганических. Это осуществляется за счет энергии, получаемой при окислении других неорганических соединений (железо- , азото-, серосодержащих веществ).

Хемосинтез был открыт русским микробиологом С.Н. Виноградским в 1888 году. Большинство хемосинтезирующих бактерий относится к аэробам, для жизни им необходим кислород.

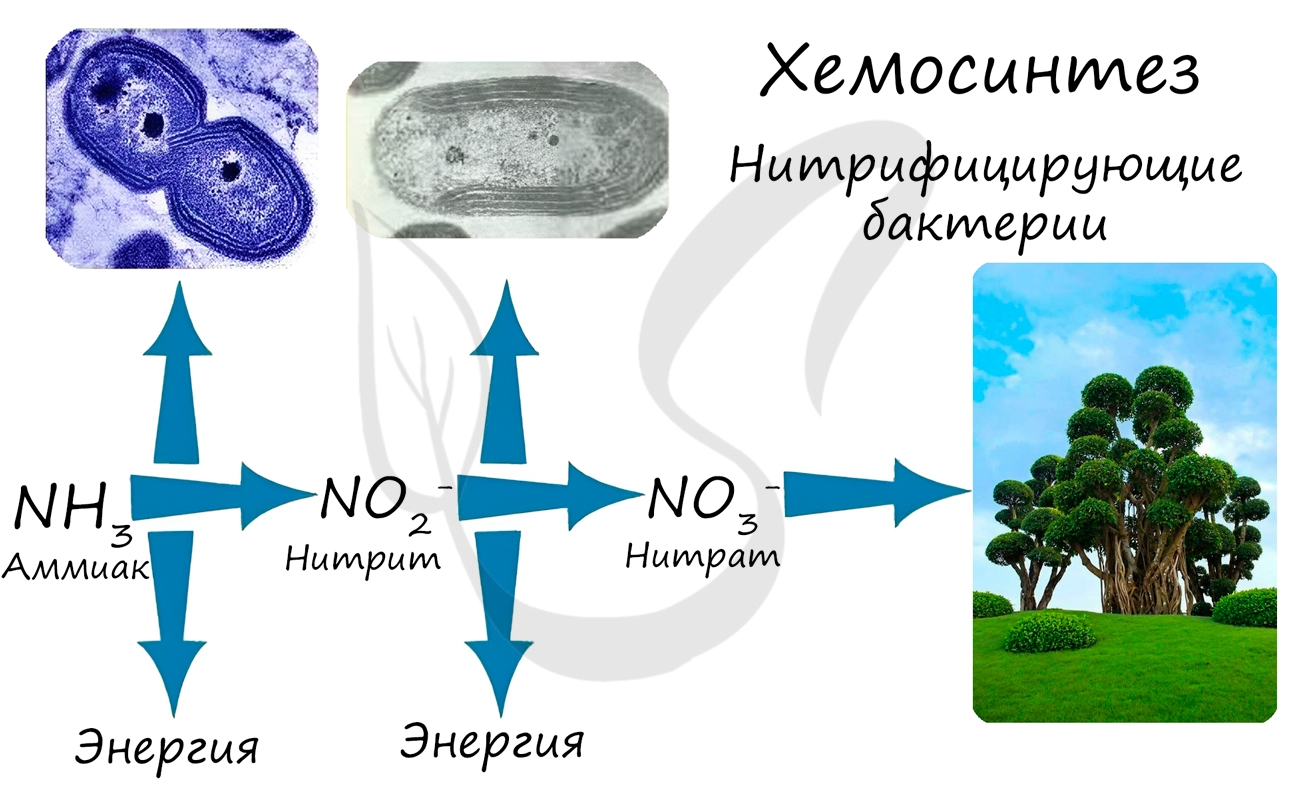
При окислении неорганических веществ выделяется энергия, которую организмы запасают в виде энергии химических связей. Так нитрифицирующие бактерии последовательно окисляют аммиак до нитрита, а затем – нитрата. Нитраты могут быть усвоены растениями и служат удобрением.

• Серобактерии – окисляют H₂S –> S 0 –> (S +4 O₃) 2- –> (S +6 O₄) 2-
• Железобактерии – окисляют Fe +2 –>Fe +3
• Водородные бактерии – окисляют H₂ –> H +1 ₂O
• Карбоксидобактерии – окисляют CO до CO₂

Значение хемосинтеза

Хемосинтезирующие бактерии являются неотъемлемым звеном круговорота в природе таких элементов как: азот, сера, железо.

Нитрифицирующие бактерии обеспечивают переработку (нейтрализацию) ядовитого вещества – аммиака. Они также обогащают почву нитратами, которые очень важны для нормального роста и развития растений.

Усвоение нитратов происходит за счет клубеньковых бактерий на корнях бобовых растений, однако важно помнить, что клубеньковые (азотфиксирующие) бактерии, в отличие от нитрифицирующих бактерий, питаются гетеротрофно.

© Беллевич Юрий Сергеевич 2018-2022

Данная статья написана Беллевичем Юрием Сергеевичем и является его интеллектуальной собственностью. Копирование, распространение (в том числе путем копирования на другие сайты и ресурсы в Интернете) или любое иное использование информации и объектов без предварительного согласия правообладателя преследуется по закону. Для получения материалов статьи и разрешения их использования, обратитесь, пожалуйста, к Беллевичу Юрию.

Рособрнадзор назвал самый сложный выпускной экзамен: итог поразил

Cпециалисты Рособрнадзора подвели итоги Единого государственного экзамена этого года. Выяснилось, что основное количество «двоек» школьники получили, сдавая предметы по выбору. Рейтинг самых сложных экзаменов возглавила биология, с ней не справились более 17% выпускников. На втором месте оказалось самое популярное у школьников обществознание, его завалили 16,4% учащихся. Бронзовую медаль по сложности завоевала химия — 15,9% двоечников.

Почему именно эти предметы вызвали у выпускников наибольшие трудности? Своим мнением поделились учителя по этим дисциплинам.

Фото: Евгений Семенов

По сравнению с 2014 годом рейтинг самых сложных экзаменов претерпел значительные изменения. Раньше самым сложным предметом для учащихся была история — тогда минимальный балл по этой дисциплине не смогли набрать более 20% ребят. В этом году история оказалась лишь на пятом месте по сложности, с ней не справились лишь 9,6% школьников. Второе место по сложности четыре года назад заняла география, а третье — все та же химия, по которой школьники стабильно не блещут знаниями.

Удивительно, что школьников, не сдавших экзамены по основным дисциплинам, оказалось в разы меньше, чем тех, кто не справился с предметами по выбору. Казалось бы, если выпускник выбирает по собственному желанию предмет, он должен его любить и неплохо знать. Однако на деле это оказалось совсем не так. По словам педагогов, такая картина сложилась из-за того, что подготовке к ЕГЭ по дополнительным предметам в школе уделяют намного меньше внимания. К тому же во многих учебных заведениях наблюдается дефицит профессиональных учителей именно обществознания, биологии и химии.

— Думаю, что причина того, что каждый шестой школьник завалил экзамен по биологии, кроется в высокой сложности данного ЕГЭ, — объясняет учитель биологии Наталья Капустина. — В данном экзамене встречаются вопросы, которые не всегда освещаются в учебниках, их просто не проходят в рамках школьной программы. При этом у детей, которые серьезно занимаются биологией дополнительно, данный ЕГЭ тоже может вызвать проблемы, так как некоторые вопросы в нем строятся на сведениях 20–30-летней давности. К сожалению, за последнее десятилетие содержание школьных пособий практически не изменилось, а ведь биология является одной из самых быстроразвивающихся наук. В связи с этим победители серьезных биологических олимпиад крайне редко набирают 100 баллов за этот ЕГЭ. Кроме того, ЕГЭ по биологии обычно сдают не более 2–3 человек из класса, поэтому только из-за них у учителя просто нет возможности давать на уроках дополнительный материал, а заниматься с репетитором есть возможность далеко не у всех. Помимо прочего в школах, особенно сельских, наблюдается серьезная нехватка педагогов по этому предмету. В ряде учебных заведений эту дисциплину и вовсе ведут учителя по другим предметам. Примерно такая же ситуация наблюдается и с учителями химии — дисциплины, которая сама по себе представляется сложной для большинства учащихся. Репетитор по обществознанию, бывший школьный учитель Антон Сомов, полагает, что большое количество школьников получают «двойки» за ЕГЭ по этому предмету из-за того, что неоправданно считают его легким. В результате многие ребята отправляются на экзамен, толком не подготовившись. А на деле просто «наболтать», отвечая на вопросы ЕГЭ, как на уроке, не получается. Ответы на вопросы должны быть развернутыми и четкими. Чтобы получить высокий балл, выпускник должен не только владеть терминологией, но и уметь логически мыслить.

— Проблема плохой подготовки школьников по обществознанию кроется еще и в недостаточном количестве профессиональных учителей по этому предмету, — объясняет репетитор. — В городских школах этот предмет подчас ведут педагоги по истории, а в сельских учебных заведениях — и вовсе кто угодно. Это очень серьезно сказывается на качестве подготовки школьников. При этом обществознание на самом деле дисциплина достаточно непростая, она представляет собой синтез философии, социологии, основ правоведения и психологии. Помимо легких тем о семье и личности встречаются сложные вопросы из области политики или права, например, те, которые требуют глубокого изучения. При этом при подготовке к ЕГЭ на уроке школьников просто натаскивают на выполнение шаблонных тестов, практически не уделяя внимания теоретической подготовке. Все это приводит к тому, что дети так часто получают низкие баллы по этому предмету.

Подготовка к окончанию университета

Заключительные экзамены в университете проходят в основном в июне. За месяц до итоговой аттестации деканат предоставляет выпускникам подробное расписание. Очень важно перед подготовкой к госэкзаменам правильно распределить время.

Полезные советы

ГИА — довольно сложное и длительное мероприятие. Спустя 4 года обучения в высшем учебном заведении студенты дневного отделения некоторый материал забыли, но достаточно повторить лекции по всем дисциплинам. Гораздо труднее выпускникам заочной формы обучения, которые, скорее всего, ни разу не открывали книги по профилирующим предметам.

Как подготовиться к ГОСам за неделю:

1. Сохраните конспекты — это значительно сэкономит время, так как не придется снова выписывать из огромных книг самые важные моменты.
2. Грамотное распределение времени — не следует пытаться за один день выучить вопросы по всем дисциплинам. Планирование поможет не только качественно вспомнить материал 4 лет обучения, но и отдыхать достаточное количество часов.
3. В качестве основных литературных источников для подготовки использовать те учебные пособия, которые предоставил университет.
4. Выработать личную схему запоминания материала (например, классифицировать вопросы по разделам).
5. Бездумно выученные ответы быстро забываются, поэтому гораздо лучше понять изучаемые темы.
6. Графическое изображение материала — полезные, компактные рисунки на учебной доске или ватмане облегчат процесс запоминания.
7. Создать образец экзаменационного билета — с закрытыми глазами выберите 3 вопроса различной тематики и ответьте на них без дополнительной помощи.
8. Писать шпаргалки полезно — работает не только зрительная, но и механическая память.

Студентам с хорошей успеваемостью вполне достаточно недели для того, чтобы выучить ответы на все вопросы. Выпускникам заочного отделения преподаватели советуют начинать готовиться к госэкзаменам за 6 месяцев. Разбить вопросы по профильным дисциплинам, делать графические схемы для быстрого запоминания.

День итоговой аттестации

Государственная аттестация бакалавров и магистров проводится на факультете, где на протяжении 4 или 6 лет учились студенты. Для проведения выпускных тестов выбирают просторную аудиторию, выделяя несколько столов для аттестационной комиссии. Подготовиться к ответу приглашают не более 6 студентов, каждому предлагается отдельный стол. В первую очередь сдают ГОСы студенты очного отделения.

Во многих университетах России распространено приготовление угощений для членов комиссии. Это, как правило, обговаривается заранее с методистом факультета, где обучались выпускники. Студенты самостоятельно не покупают продукты для преподавателей, а предварительно собирают небольшие денежные взносы.

Деканат факультета просит студентов также купить около 10−15 бутылок воды. Завершительный экзамен длится долго, так как в один день председатели комиссии могут послушать около 30 студентов. Лаборанты кафедры, на которой проводится аттестация, ставят на столы преподавателей и выпускников пластиковые стаканы.

В день ГОСов и защиты дипломной работы принято приносить букеты для преподавательского состава университета. Не стоит каждому выпускнику покупать цветы, достаточно 2−3 букетов в день экзамена от всех групп. Методисты факультета заранее готовят вазы с водой. Красивыми цветочными композициями студенты стараются задобрить комиссию, чтобы в дальнейшем получить хорошие оценки за последний экзамен.

Государственная итоговая аттестация — это завершительный этап обучения в ВУЗе. После всех переживаний и стрессов выпускников ждет долгожданная награда — диплом бакалавра или магистра. В большинстве случаев преподаватели университета помогают хорошим студентам в дальнейшей профориентации. Поэтому старательная учеба, отличные оценки за госэкзамены и дипломную работу позволят выпускникам найти достойную работу.

Дистанционное обучение в течение 4 лет мне далось очень легко, но переживания за первую встречу с преподавателями института с каждым днем становились все больше и больше. Как оказалось, последний экзамен пишется быстро. Государственная комиссия принимала экзамен без дополнительных вопросов.

Итоговая аттестация в Москве проходила очень строго. В комиссии присутствовали серьезные ученые, профессора. Списать ни у кого из группы не получилось, поэтому студенты, которые плохо учили, получили оценку 3 или вовсе пошли на пересдачу. Хоть сдача госэкзамена проходила тяжело, но это правильно, когда все получили по заслугам.

Материала для подготовки было крайне много. Я, честно сказать, не успел даже рассмотреть все вопросы из предложенного списка. Но преподаватели в комиссии были очень лояльны по отношению к студентам. Воспользоваться шпаргалками никто из сдающих студентов не пытался, так как знали, что обязательно будут дополнительные вопросы. Обращали внимание на оценки прошлых лет и участие в биологических олимпиадах, особенно областных.

Я все 6 лет обучения была старостой одной из групп заочного отделения. Преподаватели, понимая постоянную занятость студентов, делали поблажки на госэкзаменах. Но те личности, которые практически не появлялись в университете во время обучения, получили плохие оценки. Большую роль сыграл накрытый стол для аттестационной комиссии. Группа приносила в день ГОСа не только букеты, но и подарки для доцентов и профессоров. Во время подготовки к ответу у некоторых одногруппников получилось тихонько списать.

{RANDOM_PARAGRAPH=401-800}
{RANDOM_SECTION=500-3000}